I guess he only knits rectangles.
I get lots of blog hits from folks looking for shawl calculation help. Many people knitting a triangular shawl from the top down want to know how many pattern repeats they can finish before they run out of yarn. I gave a method (using algebra) in this post and a follow-up in this post.

I recently started Ene's Scarf, my first triangular scarf/shawl knit from the bottom up. Meaning: cast on a terrific number of stitches, then decrease regularly until they are almost all gone, bind them off and block out to triangular shape.
Again, this isn't really a triangle, but a trapezoid. Cast on 375 stitches, decrease two stitches per row until you are left with 19 stitches, then do a bind-off that grafts them together.
This time, I know I have enough yarn. (Elsebeth Lavold's Silky Wool. Purchased to make Cozy from knitty.com, frogged for a variety of reasons.) All I really want to know is when I have reached the halfway point for the psychological assurance. However, if I were worried about having enough yarn, I would use the same calculations --- but factoring in the extra yarn used in the cast-on row more carefully.
First: Draw a picture and determine what I know and what I want to know.
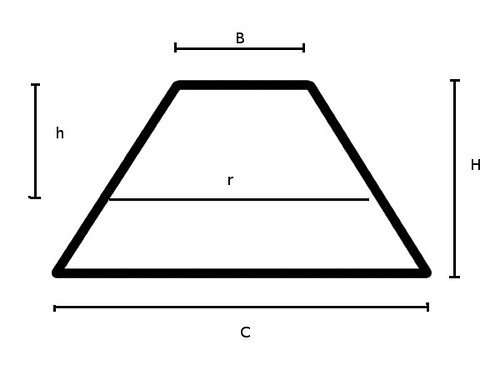
For Ene's Scarf:
C = cast on = 375 stitches
B = end (not exactly bind-off, but close enough) = 19 stitches
H = number of rows = 179
note that if one really does decrease two stitches per row, the numbers are a teeny bit off -- one would end up with 17 stitches. That's because in this pattern, there are a few rows that don't follow the rules completely, but the difference is negligible for my needs.
Total number of stitches = Area of trapezoid = 1/2(C+B)*H = 35,263
I know that I will have knit half the scarf when I reach row h with r stitches where the area of the top trapezoid with base r is exactly half the area of the whole trapezoid.
I have two unknowns, h and r. Fortunately, I can solve for r in terms of h, so I will end up having an equation with one unknown and I can solve it.
h = rows left to finish
r = number of stitches in the row where there are h rows left.
So r = 19 + 2h
Area of top trapezoid is 1/2(19 + r) * h = 1/2(19 + 19 + 2h)h = 19h + h²
So we have to solve for h where
19h + h² = 1/2(35,263) = 17,631.5
h² + 19h - 17,631.5 = 0 is a quadratic equation, easily solved by the Pythagorean Theorem.
Do you want to see the calculations? I thought not. But I'll show you anyway. There are two real solutions to this equation, but we are only interested in the positive solution. Therefore, we only care about
(-19 + (19² - 4 * (-17,631.5))^.5) / 2 = 124 (more or less)
I will be halfway done when I have 124 rows left. 179 rows total, means I will be halfway done when I have finished 55 rows.

5 comments:
Oh. My. Goddess. I am so glad I have you in my life. Even tho I have a math degree, I'm not sure I would have the patience to figure that out. (Actually, I would, but I would make a careless arithmetical mistake & come out with an obviously incorrect answer, like 2.)
Actually, until I read your blog posts about calculating yarn needs, it never would have occurred to me to try doing so if I were in doubt. Now I know that I can do it myself and not just rely on a pattern.
Also, just for the record, I really wish I had studied foreign languages in college. I am not a true math person, altho I did well while I was there. I just simply hated analysis, and you can't really be a mathematician without getting analysis.
This message brought to you by COFFEE!!!
Nobody can really live without algebra, they just don't know they use it.
I remember quite well how you and I discovered algebra together before ever hearing the term.
Well, with THAT kind of logic, we should stop teaching history, nobody ever uses that in real life. And science, who needs to know the earth revolves around the sun, that's useless in everyday life. What DOES he think we should be teaching???
For heaven's sakes.
"...he only knits rectangles." Hee hee!
I didn't follow your analysis closely, just skimmed it, because I'm pretty sure I could figure it out, too. (Although like your cousin Jane, I too would make a silly arithmetic mistake somewhere.) And I absolutely hate following through someone else's analysis -- way too much like work. But good for you. Being math-enabled is A Good Thing. Very useful.
Would this be my cousin Jane and my sister, Maggie on here? Cool!
Hi guys! We'll leave Germany in a couple of months - back to VA...
...where maybe I'll start to knit something other than scarves!
Math is fun. I shouldn't have gotten a degree in it either, Jane. But I could do it so I just kept on doing it. lol
I like Algebra so much I am considering tutoring as a part time job. So many kids struggled with it here - and their parents plead with me to help me when they realize I have a degree.
I'll suggest to my son that he should go the language route. He's pretty fluent in German now - and also good at math! Must be in the genes.
Smiles, Teresa
Post a Comment