More fun with mathematics (and knitting)

Just about anyone with a school-aged child is aware of the controversies in mathematics education. As a former math teacher and the parent of a ninth grader, I follow it pretty closely. The other day I read an article from a fellow arguing that algebra ought to be an elective in high school, that not many people ever have to use algebra in real life, so why make everyone suffer through it. He was especially critical of word problems and claims that there are no real life word problems that anyone would ever want or need to solve.

I guess he only knits rectangles.

I get lots of blog hits from folks looking for shawl calculation help. Many people knitting a triangular shawl from the top down want to know how many pattern repeats they can finish before they run out of yarn. I gave a method (using algebra) in this post and a follow-up in this post.



I recently started Ene's Scarf, my first triangular scarf/shawl knit from the bottom up. Meaning: cast on a terrific number of stitches, then decrease regularly until they are almost all gone, bind them off and block out to triangular shape.

Again, this isn't really a triangle, but a trapezoid. Cast on 375 stitches, decrease two stitches per row until you are left with 19 stitches, then do a bind-off that grafts them together.

This time, I know I have enough yarn. (Elsebeth Lavold's Silky Wool. Purchased to make Cozy from knitty.com, frogged for a variety of reasons.) All I really want to know is when I have reached the halfway point for the psychological assurance. However, if I were worried about having enough yarn, I would use the same calculations --- but factoring in the extra yarn used in the cast-on row more carefully.

First: Draw a picture and determine what I know and what I want to know.




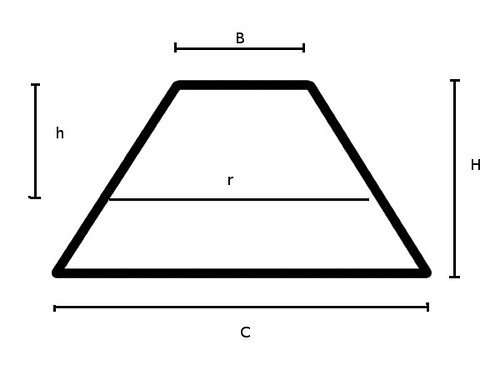
For Ene's Scarf:

C = cast on = 375 stitches
B = end (not exactly bind-off, but close enough) = 19 stitches
H = number of rows = 179

note that if one really does decrease two stitches per row, the numbers are a teeny bit off -- one would end up with 17 stitches. That's because in this pattern, there are a few rows that don't follow the rules completely, but the difference is negligible for my needs.

Total number of stitches = Area of trapezoid = 1/2(C+B)*H = 35,263

I know that I will have knit half the scarf when I reach row h with r stitches where the area of the top trapezoid with base r is exactly half the area of the whole trapezoid.

I have two unknowns, h and r. Fortunately, I can solve for r in terms of h, so I will end up having an equation with one unknown and I can solve it.

h = rows left to finish
r = number of stitches in the row where there are h rows left.

So r = 19 + 2h

Area of top trapezoid is 1/2(19 + r) * h = 1/2(19 + 19 + 2h)h = 19h + h²


So we have to solve for h where

19h + h² = 1/2(35,263) = 17,631.5

h² + 19h - 17,631.5 = 0 is a quadratic equation, easily solved by the Pythagorean Theorem.

Do you want to see the calculations? I thought not. But I'll show you anyway. There are two real solutions to this equation, but we are only interested in the positive solution. Therefore, we only care about

(-19 + (19² - 4 * (-17,631.5))^.5) / 2 = 124 (more or less)

I will be halfway done when I have 124 rows left. 179 rows total, means I will be halfway done when I have finished 55 rows.